Le principe de mesure des marégraphes acoustiques est expliqué dans le chapitre II et décrit dans la figure 12. Le signal acoustique est émis par un appareil situé au-dessus du plan d'eau. Le faisceau est émis avec un angle d'ouverture de quatre à cinq degrés. L'onde se propage aussi bien dans un tube en plastique spécifique de faible diamètre ou à l'air libre. Des mesures élémentaires sont effectuées à une cadence élevée de l'ordre de la seconde. Une moyenne sur plusieurs minutes est calculée à partir de ces mesures élémentaires, elle constitue la donnée du marégraphe. C'est une mesure intégrée sur quelques minutes qui est répétée toutes les heures par exemple. Un avantage de cette procédure est qu'elle filtre de manière satisfaisante les fluctuations de courte période du niveau de la mer sans recourir à un puits de tranquilisation. Elle permet par la même occasion de calculer des paramètres de qualité de la mesure, de rejeter les mesures élémentaires aberrantes, etc. La hauteur d'eau est déduite de la relation suivante, en respectant les notations de la figure 12:
Equation (E.VIII.1)
Les sources potentielles d'erreurs systématiques sont:
* la température, la pression atmosphérique et l'humidité relative qui influent sur la valeur de la vitesse de propagation de l'onde acoustique;
* la qualité de la mesure de temps;
* et la stabilité du centre de phase moyen de l'émission et la réception de l'onde par le senseur acoustique.
La vitesse de l'onde acoustique peut s'exprimer en fonction des paramètres cités ci-dessus par la relation du Bureau des Longitudes [Dupuy, 1993]:
Equation (E.VIII.2)
avec S : la vitesse de l'onde sonore en m/s;
P : la pression barométrique en hPa;
T : la température en °C.
A partir de cette formule, une étude simple montre que la vitesse de propagation de l'onde sonore est beaucoup plus sensible aux erreurs introduites par les variations de température que par celles de la pression atmosphérique et de l'humidité relative de l'air. En effet, des variations extrêmes de l'humidité et de la pression, [[Delta]]U=90% et [[Delta]]P= 300hPa, introduisent des erreurs de quelques millimètres. Si la précision recherchée est millimétrique, l'utilisation de la formule du Bureau des Longitude (BDL) conjuguée à des mesures classiques de pression barométrique et d'hygrométrie est satisfaisante.
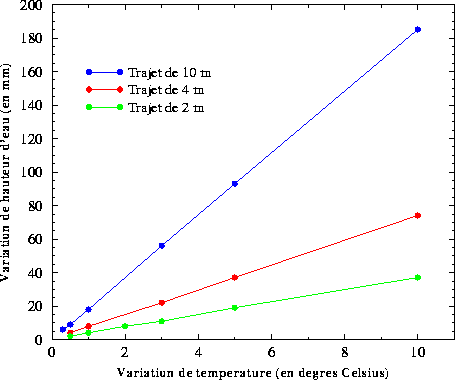
L'analyse de la formule du BDL montre que la sensibilité de la vitesse de l'onde sonore est d'environ 0.185% par degré Celsius de variation. Cette valeur s'accorde en outre avec celles que nous pouvons rencontrer dans la littérature [Gill et al 1993, IOC 1994]. Les courbes de la figure 89 donnent une idée de l'erreur commise sur la détermination de la hauteur du plan d'eau losqu'on utilise une vitesse du son constante qui ne tient pas compte de l'effet de la température.
Figure 89 : Influence de la variation de température sur la détermination de hauteur d'eau à partir d'un marégraphe acoustique dont on suppose que l'onde se propage à vitesse constante dans l'air (S=344m/s) sur des trajets de 10, 4, et 2 mètres.

Au regard de ces chiffres, il apparaît qu'une faible variation de la température génère des erreurs non négligeables sur les hauteurs d'eau. Par exemple, une variation de seulement un demi degré provoque déjà une erreur d'environ un centimètre sur un trajet de dix mètres. Plusieurs solutions sont mises en oeuvre par les divers organismes qui emploient cette technologie. En France, le SHOM mesure la température en un point du trajet de l'onde sonore, et applique une correction dérivée de la relation du BDL [Dupuy, 1993]. Aux Etats-Unis, le National Ocean Service dispose d'un appareil acoustique dont l'onde se propage à l'intérieur d'un tube en plastique de 1.3 cm de diamètre. Ce guide d'onde présente une discontinuité, en l'occurrence un petit trou, à une distance connue de la source sonore. Une partie de l'onde incidente est réfléchie au niveau du trou par effet d'impédance acoustique, tandis que le reste du signal poursuit son trajet. Une simple règle de trois permet ensuite de s'affranchir de l'inconnue de vitesse du son [Gill et al, 1993]. Enfin, en Australie, le National Tidal Facility emploie une méthode analogue à celle du NOS. La propagation du signal se faisant à l'air libre ou dans un tube en PVC de 25 cm de diamètre, une barre réflective est située à 75 cm de la source sonore [Homes, 1992]. Ces procédures de correction ne tiennent toutefois pas compte de l'effet du gradient vertical de température qui de fait peut exister le long du trajet de l'onde, notamment lorsque des effets d'ombre ont lieu. Les solutions envisagées sont de placer plusieurs capteurs de température le long du trajet, ou encore de discontinuités.
En ce qui concerne la mesure de temps de propagation du signal acoustique, signalons simplement que sa précision doit être de l'ordre de 0.01 milliseconde pour garantir une précision millimétrique de la hauteur d'eau. Quant à la stabilité du centre de phase de l'instrument, elle dépend bien entendu des caractéristiques intrinsèques au matériel du senseur. Les comparaisons menées par le SHOM entre les résultats de leur appareil acoustique prototype et un marégraphe à flotteur et d'une jauge à pression, ne montrent aucune dérive significative supérieure au centimètre entre 1990 et 1992. Gill et al [1993] montrent que les contrôles d'étalonnage effectués sur 53 marégraphes NGWLMS ne révèlent pas d'écarts supérieurs à six millimètres, la plupart étant d'ailleurs inférieurs à deux millimètres. Si ces résultats perdurent sur de longues périodes, les marégraphes à ultrasons fourniront des observations fiables pour les études de variations du niveau de la mer à long terme. L'écart-type d'une donnée intégrée sur quelques minutes est typiquement de l'ordre du centimètre.
Le puits de tranquilisation est un élément indissociable du marégraphe mécanique à flotteur. Néanmoins, il est également utilisé avec d'autres types d'appareil. C'est pourquoi nous avons distingué les erreurs systématiques des puits de la section dédiée aux erreurs des marégraphes à flotteur.
Le puits de tranquilisation amortit les fluctuations du niveau de la mer de haute fréquence, à savoir, la houle, les vagues, les clapotis, etc. En toute rigueur, il devrait agir comme un filtre dit " passe-bas ", qui n'altère pas les signaux de basse fréquence, mais qui élimine les signaux dont la fréquence est supérieure à la fréquence de coupure (cf. figure 14). En pratique, la réponse n'est malheureusement pas souvent linéaire. Elle dépend de la forme et des dimensions relatives du puits et de l'orifice, mais aussi de facteurs extérieurs comme l'envasement, la présence de vagues ou de courants. Les effets sont alors fonction de leurs caractéristiques propres d'amplitude, de période ou d'intensité.
Lennon & Mitchell [1993] montrent en particulier que l'effet des vagues est de l'ordre de 7 cm pour une oscillation de un mètre d'amplitude et sept secondes de période, mais l'effet peut atteindre 10 à 15 cm pour des vagues plus importantes [Simon, 1986]. Par ailleurs, un courant d'une intensité normale de 0.5 m/s induit dans un puits conique classique un abaissement de l'ordre de 4 cm [Lennon & Mitchell, 1993]. Simon [1986] rapporte à ce sujet des écarts de niveau de la mer s'abaissant jusqu'à 18 cm pour un courant perpendiculaire à l'axe de l'orifice du puits de 1.5 m/s. La différence de densité entre les eaux du puits et l'extérieur se traduit naturellement par une différence de hauteur d'eau. Le phénomène est fréquent à proximité des embouchures fluviales, d'autant que l'orifice du puits est petit et que le renouvellement de l'eau ne s'effectue pas complètement. L'effet peut se monter à plusieurs centimètres [Simon, 1986].
