Outre l'établissement de séries temporelles cohérentes de positions qui pourront être exploitées avec une certaine marge de liberté par les géophysiciens, ces derniers peuvent également tirer parti des vitesses calculées dans l'ITRF. Pour nous faire une première idée de la confiance attribuée à ces vitesses, mais aussi de l'évolution de leur qualité, nous avons étudié les statisques associées aux champs de vitesse des solutions ITRF dans les rapports d'analyse de l'IERS. Elles sont résumées de la même façon que dans les tableaux des figures 74 et 75 en distinguant, lorsque l'information était disponible, les composantes horizontale et verticale.
Figure 78 : Moyenne et intervalle d'amplitude par technique spatiale des résidus pondérés des combinaisons de vitesses ITRF, regroupés par solutions individuelles, en distinguant les composantes horizontales et verticales lorsque cette distinction est disponible dans les rapports techniques de l'IERS. (Valeurs en mm/an).
Technique ITRF91 ITRF92 hor. ITRF92 vert. hor. ITRF93 vert.
VLBI 1.1 [0.9 1.1 [0.7 0.8 [0.6 1.8 [0.5 0.7 [0.3 1.9 [0.7
; 1.5] ; 1.5] ; 1] ; 2.9] ; 1.2] ; 3.1]
SLR 4.5 [2.7 2.4 [0.9 2.4 [1.1 3.2 [2.3 2.3 [1.7 5.1
; 5.9] ; 4.8] ; 5] ; 4.6] ; 3]
GPS --- --- --- --- (5.7) (10.6)
Moyenne 2.8 mm/an 1.8 mm/an 1.6 mm/an 2.5 mm/an 1.5 mm/an 3.5 mm/an
Note: Ces statistiques ne sont pas disponibles pour l'ITRF94, car son champ de vitesse a été calculé à partir des résultats des deux combinaisons globales de jeux de coordonnées effectuées respectivement aux dates de référence 1988.0 et 1993.0
Afin d'étudier la qualité du champ de vitesse de l'ITRF94, nous avons récupéré les vitesses verticales relatives à cette solution. L'annexe C donne les vitesses et les écart-types de chaque point. Les informations sont regroupées par sites géographiques et nous rappelons en outre la catégorie du point considéré (A,B,C ou Z). L'histogramme de la figure 79 donne une idée générale de la précision des vitesses de l'ITRF94. Cette précision est estimée par l'écart-type correspondant, obtenu du calcul de combinaison par moindres carrées. On constate que le mode principal se situe autour de 1 à 2 mm/ an, mais que seulement 38% des vitesses sont déterminées avec un écart-type inférieur à 2 mm/an; 67% étant déterminées à mieux que 4 mm/an.
Figure 79 : Histogramme de la précision des vitesses verticales de l'ITRF94.
Les histogrammes des figures suivantes 80 et 81 détaillent les résultats par technique et par classe de qualité des points. Des 242 points qui disposent d'une vitesse dans l'ITRF94, 86 points sont déterminés par VLBI, 62 par SLR, 52 par GPS, et 42 par DORIS. Toutes les techniques présentent un mode principal situé entre 1-2 mm/an, bien qu'il soit moins évident pour DORIS. En outre, 71% des vitesses GPS sont évaluées avec un écart-type inférieur à 3 mm/an. Du côté des techniques SLR et VLBI, un niveau de précision équivalent est atteint respectivement pour 63 % et 59% des stations, alors que la précision des vitesses DORIS reste assez hétérogène.
Par ailleurs, les 242 points se répartissent dans les trois premières classes de qualité que nous avons défini auparavant : 66 en classe `A', 71 en classe `B', et 105 en classe `C'. Les premières catégories présentent un mode principal de l'ordre de 1-2 mm/an, alors que celui de la catégorie `C' se situe plutôt entre 2-3 mm/an. Aussi, on constate que 77% des vitesses regroupées dans `A' sont déterminées avec un écart-type inférieur à 2 mm/an. Le même niveau de précision est atteint pour 41% des vitesses de la classe `B', et seulement pour 10% des vitesses de la classe `C'.
Figure 80 : Histogrammes de la précision des vitesses verticales de l'ITRF94 regroupées par technique de géodésie spatiale.
Figure 81 : Histogrammes de la précision des vitesses verticales de l'ITRF94 regroupées par classes de qualité (A,B ou C).
Nous avons étudié la précision relative de l'estimation des vitesses ITRF94 à partir de l'analyse du coefficient de variation, défini comme le rapport de l'écart-type à la valeur absolue de la variable aléatoire considérée (cf. relation E.II.9). Plus ce coefficient est faible et meilleure est la qualité de l'estimation. En effet, la figure 82 montre que, dans le cas d'une variable aléatoire gaussienne, un coefficient de variation de 1/5 permet de déterminer de manière certaine le signe de la variable. Un coefficient de 1/2 permet de connaître le signe avec une probabilité encore importante d'environ 98%, en revanche pour un coefficient de 1, la probabilité se réduit à environ 83,5%.
Figure 82 : Evaluation de la précision relative de l'estimation d'une variable aléatoire à partir de l'étude du coefficient de variation. (Nous considérons ici une distribution gaussienne).
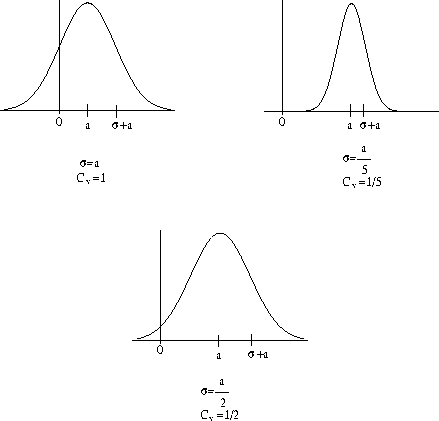
Si l'on considère que la variable suit une loi de probabilité quelconque, un coefficient de variation supérieur à 1/2 ne permettra pas a priori de discriminer, avec un niveau de confiance statistique d'au moins 75% [Bougeard, 1990], si la grandeur vraie que l'on cherche à estimer est positive ou négative. Les coefficients de variation des vitesses verticales estimées dans l'ITRF94 sont fournies dans la dernière colonne du tableau de l'annexe C.
L'histogramme de la figure 83 indique un mode principal de 0.5-0.75 pour le coefficient de variation calculé sur les vitesses verticales de l'ITRF94. Il convient toutefois de noter que seulement 16% des vitesses ont un coefficient inférieur à 0.5, et 35% un coefficient inférieur à l'unité.
Figure 83 : Histogramme du coefficient de variation calculé pour les vitesses verticales estimées dans l'ITRF94.
Si l'on regarde le détail des résultats par technique spatiale, la figure 84 montre que le pourcentage des vitesses VLBI ayant un coefficient de variation inférieur à 0.5 est de 19%, il est de 16% pour les vitesses SLR, de 15% pour les vitesses GPS, et de 10% pour les vitesses DORIS. Lorsque l'on regarde les résultats pour un coefficient de variation inférieur à l'unité, nous trouvons 36% des vitesses VLBI, 39% des vitesses SLR, 44% des vitesses GPS, et 17% des vitesses DORIS.
Enfin, la figure 85 conforte quelque peu le classement de qualité des points de l'ITRF94 puisque 12% et 41% des vitesses de catégorie A ont des coefficients de variation inférieurs à 0.5 et 1 respectivement, contre 24% et 49% pour les vitesses de classe B, et 11% et 21% pour les vitesses de classe C.
Figure 84 : Histogrammes du coefficient de variation calculé pour les vitesses verticales estimées dans l'ITRF94 et regroupées par technique de géodésie spatiale.
Figure 85 : Histogrammes du coefficient de variation calculé pour les vitesses verticales estimées dans l'ITRF94 et regroupées par classes de qualité (A,B ou C).
Plusieurs éléments ressortent de cette brève analyse. D'abord, la précision des vitesses verticales de l'ITRF94 s'avère, en termes d'écart-type, inférieure à 2 mm/an dans presque 40% des cas. Deux tiers des vitesses sont évaluées à mieux que 4 mm/an. Au regard de l'indicateur de qualité fourni par le coefficient de variation, il semble ensuite que les vitesses soient encore peu significatives. Dans au moins 65% des cas, nous ne sommes pas en mesure de discriminer si le point fait l'objet d'un affaissement, ou d'un soulèvement, avec un niveau de confiance statistique d'au moins 75%. Il est toutefois possible que les points soient effectivement stables, auquel cas cet indicateur relatif de qualité paraîtra toujours trop fort, ceci quelque soit la précision absolue de l'estimation. Rappelons par ailleurs que les mesures précises sont récentes, et par conséquent trop brèves pour fournir des résultats clairs et significatifs. Il est donc encore difficile de les interpréter comme des mouvements réels de l'écorce terrestre. C'est ainsi que la technique spatiale DORIS, récemment introduite dans le calcul de l'ITRF, donne en général des estimations moins fiables.
Si l'incertitude des vitesses ITRF94 paraît encore un peu large, nous ne devons pas oublier que nous cherchons à estimer le niveau d'exactitude des résultats. La précision affichée par les centres d'analyse est de fait bien inférieure car elle est évaluée en interne. De plus, les critères sont souvent fondés sur une théorie statistique qui suppose l'absence d'erreurs systématiques. La comparaison et la combinaison des solutions inter-centres et inter-techniques est à cet égard précieuse pour prendre conscience des problèmes. Notons toutefois que ces analyses comparatives dépendent fortement de la qualité liens mesurés localement entre les points d'un même site. Aujourd'hui, les rattachements locaux semblent en effet limiter la qualité des combinaisons des solutions globales individuelles. Leur précision est dans de nombreux cas insuffisante, et il devient nécessaire de prendre en compte par ailleurs leur évolution temporelle.
Nous avions songé dans un premier temps à effectuer un travail complémentaire à celui du chapitre II en corrigeant nos résultats marégraphiques par la donnée de vitesses verticales issues de la géodésie spatiale et disponibles dans l'ITRF94. L'hypothèse de départ entrevue était l'identification du mouvement vertical observé par la station de géodésie spatiale à celui du repère de marée. Cependant, au regard des résultats actuellement fournis par la géodésie spatiale et de la distance souvent considérable qui sépare les points géodésiques concernés des marégraphes intéressants de notre étude, nous avons abandonnée cette idée pour l'instant. Le tableau de l'annexe D donne la distance qui sépare les marégraphes de plus de 40 données annuelles de type RLR du PSMSL, de la station ITRF94 la plus proche. Aussi, des 200 marégraphes considérés, 98 ont un point de l'ITRF94 à moins de 200 km, dont 29 GLOSS. Seuls 30 marégraphes ont un point ITRF94 à une distance de 50 km, dont 7 GLOSS, mais parmi ces points, 9 ne fournissent pas d'estimation de vitesse dans l'ITRF94, dont 2 GLOSS.
Ces données montrent que peu de stations de géodésie spatiale sont à proximité des marégraphes. Les intérêts propres à la géodésie ne coïncident manifestement pas souvent avec ceux de la marégraphie. Un effort spécifique est par conséquent nécessaire si l'on souhaite corriger de manière satisfaisante les tendances apparentes du niveau de la mer déterminées à partir des marégraphes. En outre, il s'avère qu'au sein d'un même site les vitesses verticales ITRF94 diffèrent parfois de plus de 1 mm/an. Ces écarts pourraient traduire des déformations locales différentielles entre points, mais les valeurs des vitesses restent toutefois cohérentes avec leur fourchette d'incertitude. L'hypothèse d'un mouvement vertical identique entre le point géodésique et le repère de marée est par ailleurs audacieuse, mais surtout peu rigoureuse au regard de la variété des mouvements physiques possibles à l'échelle locale, d'une part, et du niveau de précision considéré, d'autre part, d'autant que la distance qui les sépare s'accroît.
