Le système de référence terrestre ITRS permet en particulier une détermination réaliste des déformations de l'écorce terrestre. A cet égard, il est intéressant de noter que, dans de nombreux sites, les vitesses horizontales obtenues par géodésie spatiale sont en bon accord avec les déplacements des plaques tectoniques estimés sur quelques millions d'années à partir des enregistrements géologiques. Les graphiques fournis par Boucher et al [1996] dans leur analyse de l'ITRF94 montrent d'ailleurs que cet accord est surtout visible pour les points éloignés des frontières de plaques qui ne sont pas affectés par d'autres causes de mouvement. Les résultats de géodésie spatiale servent désormais à l'élaboration des modèles de mouvement des plaques tectoniques [DeMets et al, 1996], puisque ces mouvements s'avèrent fondamentalement linéaires sur des périodes de temps géologiques.
Toutefois, force est de constater que la composante verticale est dans la plupart des cas moins bien déterminée. Cette remarque est illustrée dans le tableau de la figure 75, établi d'une manière analogue à celui de la figure 74, en considérant les résidus pondérés donnés suivant les composantes horizontale et verticale, lorsqu'ils étaient effectivement disponibles. Les sources d'erreur systématiques potentielles qui pourraient expliquer cette anisotropie sont diverses, nous les verrons plus en détail dans un prochain chapitre.
Figure 75 : Moyenne et intervalle d'amplitude par technique spatiale des résidus pondérés des combinaisons de coordonnées ITRF, regroupés par solutions individuelles, en distinguant les composantes horizontales et verticales, fournis dans les rapports techniques de l'IERS. (Valeurs en cm. L'astérisque indique qu'il s'agit de résultats obtenus pour une combinaison à la date de référence 1993.0 au lieu de 1988.0).
Technique hor. ITRF92 vert. hor. ITRF93* vert. hor. ITRF94* vert.
VLBI 0.6 [0.3 1.3 [0.8 0.5 [0.4 0.8 [0.7 0.5 [0.3 1.3 [0.6
; 1.1] ; 2.6] ; 0.6] ; 0.9] ; 0.8] ; 3.2]
SLR 2.4 [1.3 3.3 [1.9 1.9 2.4 0.8 1.2
; 4.8] ; 7.2]
LLR 3.8 [3.6 3.0 [2.2 --- --- --- ---
; 4.3] ; 3.5]
GPS 1.2 [0.4 1.9 [0.8 0.8 [0.5 1.6 [1.1 1.0 [0.3 2.1 [0.8
; 3.1] ; 4.4] ; 1.1] ; 2.2] ; 2] ; 4.7]
DORIS --- --- --- --- 2.2 [1.8 2.3 [2 ;
; 2.8] 2.8]
Moyenne 2 cm 2.4 cm 1 cm 1.6 cm 1.1 cm 1.7 cm
Les relations (E.VI.4) et (E.VI.5) rappellent les transformations entre systèmes de coordonnées cartésiennes (x,y,z) et géographiques ([[lambda]],,h):
Equation (E.VI.4)
et dans le sens inverse, nous avons:
Equation (E.VI.5)
Les réalisations successives de l'ITRS présentent des paramètres de transformation non nuls entre elles. Le tableau de la figure 76 donne la valeur des paramètres de translation et d'échelle entre la solution ITRF94 à la date 1988.0 et les solutions précédentes à la même date de référence [Boucher et Altamimi, 1996]. Chaque solution, la meilleure possible au moment du calcul, définit en toute rigueur un repère intrinsèque. Néanmoins, les écarts systématiques entre ces solutions reflètent plutôt l'effet des données considérées, l'amélioration des analyses et des modèles. La dernière solution serait ainsi la plus fiable.
Figure 76 : Evolution des paramètres de translation et d'échelle entre la solution ITRF94 du repère conventionnel de l'IERS, à la date 1988.0, et les solutions précédentes, à la même date de référence, d'après Boucher et Altamimi [1996].
Paramètre ITRF88 ITRF89 ITRF90 ITRF91 ITRF92 ITRF93 T1 (cm) 1.8 2.3 1.8 2.0 0.8 0.6 T2 (cm) 0 3.6 1.2 1.6 0.2 -0.5 T3 (cm) -9.2 -6.8 -3.0 -1.4 -0.8 -1.5 D (10-8) 0.74 0.43 0.09 0.06 -0.08 0.04
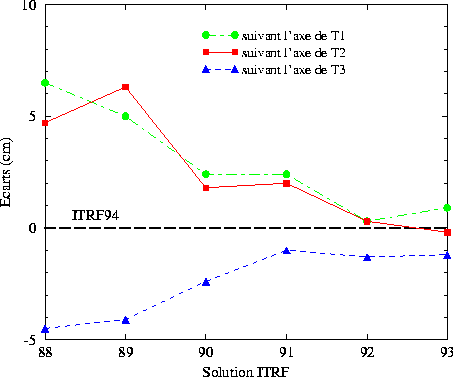
La figure 77 montre la variation verticale de la position de trois points à la surface de la Terre suivant que leurs coordonnées sont exprimées dans un repère ITRF ou dans un autre. Les points considérés sont idéalement situés sur chacun des axes du repère et ne subissent en théorie aucune déformation réelle. L'ITRF94 est traité ici comme une référence parfaite. Les écarts de position ITRFYY-ITRF94 proviennent alors de l'effet artificiel et cumulé de la variation de l'échelle et du géocentre entre les solutions successives.
Les courbes confirment l'idée que les réalisations de l'ITRS convergent vers une solution numérique plus exacte qui se stabilise dans le temps au niveau centimétrique. Aussi, il est important de considérer la dernière solution de l'ITRF lorsque l'on cherche à établir des séries temporelles de positions à la surface terrestre, d'autant que l'on souhaite les interpréter par la suite d'un point de vue géophysique. Par conséquent, afin d'éviter les effets artificiels introduits par les calculs successifs du repère de référence, il est indispensable d'exprimer une série temporelle de manière cohérente dans un repère unique de qualité supérieure. Cela suppose donc de recalculer les positions obtenues dans le passé par la technique de géodésie spatiale considérée, ou encore, de leur appliquer les paramètres de transformation adéquats.
Figure 77 : Variations de la position de trois points à la surface de la Terre (a6378137 m) suivant qu'ils sont exprimés dans un repère ITRF ou dans un autre. Les écarts sont dus à l'effet cumulé de la variation de l'échelle et du géocentre. (Les points sont situés sur chaque axe du repère. L'ITRF94 est considéré parfait).

