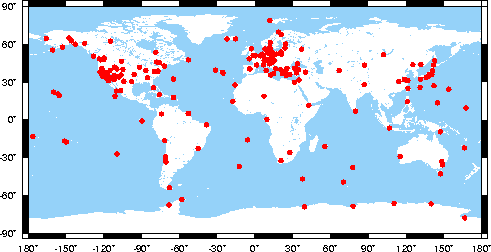
A ce jour , sept solutions se sont succédées pour réaliser le système de référence terrestre de l'IERS, et concrétiser le repère conventionnel associé. Chacune est identifiée par le sigle générique ITRF suivi d'un nombre correspondant à l'année des observations les plus récentes, parmi celles qui ont servi à effectuer les calculs. Il s'agit en l'occurrence des solutions ITRF88, ITRF89, ITRF90, ITRF91, ITRF92, ITRF93, ITRF94. Les analyses et les résultats sont décrits dans les notes techniques de l'IERS. La figure 73 montre la répartition des 201 sites qui constituent l'ITRF94. Parmi ces sites, 104 comprennent du VLBI, 62 du SLR, 66 du GPS, 52 du DORIS, et 3 du LLR, bien qu'aucune solution de cette dernière technique ne fut utilisée dans la combinaison finale [Boucher et al, 1996].
Figure 73 : Répartition des 201 sites de la solution ITRF94 du repère conventionnel de l'IERS.

La stratégie de combinaison des jeux de coordonnées a considérablement évolué depuis l'ITRF88. Elle s'appuie sur l'appréciation la plus juste possible de la sensibilité naturelle de chaque technique spatiale aux différents éléments du système de référence, d'une part, et de la qualité observée dans les jeux individuels fournis par les centres d'analyse, d'autre part. C'est ainsi que, par exemple, les origines des solutions ITRF88 à ITRF93 étaient fixées à celles des solutions SLR successives du centre de recherche spatiale de l'Université du Texas, alors que l'origine de l'ITRF94 est une moyenne pondérée des origines de jeux SLR et GPS. Ces choix stratégiques sont revus dans un article de Boucher et Altamimi [1996] pour chacun des éléments du système. Par ailleurs, l'analyse des jeux de coordonnées individuels et de leurs matrices de covariance associées a conduit les chercheurs du LAREG impliqués dans l'IERS à revoir à plusieurs reprises les pondérations des données dans leur combinaison globale. En effet, les matrices de covariance fournies par les centres d'analyse s'avèrent parfois trop pessimistes, parfois trop optimistes au regard des résultats statistiques obtenus des comparaisons et des combinaisons préalables des jeux reçus [Boucher et Altamimi, 1993]. Elles ne sont donc pas utilisées directement comme pondération des données dans le calcul final. A cet égard, l'établissement de la stratégie de pondération est un travail délicat et quelque peu laborieux, qui a notablement évolué [Sillard, 1997-a].
Au cours de ces dernières années, les techniques de géodésie spatiale, les méthodes et les modèles de traitement et de réduction des données ont beaucoup progressé. Des nouveaux systèmes de positionnement sont venus participer à la construction de l'ITRS depuis 1991, GPS et DORIS, et les liens entre techniques dans les sites en colocation se sont multipliés, apportant une meilleure couverture. Aussi, il est légitime de penser que la dernière solution de l'ITRF est de meilleure qualité que les précédentes. De fait, chacune des réalisations du système définit un repère intrinsèque, si l'on considère que deux repères sont rigoureusement identiques lorsque les paramètres de transformation qui les lient sont nuls. Nous verrons plus loin que ces paramètres sont en effet non nuls. Une première explication est que, par nature, nos réalisations numériques sont imparfaites. Des raisons plus spécifiques et techniques pourraient être évoquées, comme par exemple la date centrale différente des lots de mesures, ou encore, les contraintes de fixation appliquées dans un calcul d'orbite. La première semble en effet influer sur l'origine du repère, alors que la deuxième affecte son orientation en raison de la corrélation entre l'axe du pôle de rotation terrestre et l'axe `z' du repère. Les explications possibles sont diverses et variées. Elles relèvent souvent de l'application de modèles, de constantes, etc. qui ne sont pas rigoureusement identiques. Le choix de la constante de gravitation géocentrique se répercute par exemple sur l'échelle du repère. Une erreur systématique de caractère global dans un jeu de coordonnées individuel peut donc se retrouver dans un des paramètres de transformation lors de l'ajustement par moindres carrés.
Outre l'adoption de l'ITRS par l'UGGI depuis 1991, la qualité de la réalisation de ce système de référence terrestre se reflète dans l'élaboration des conventions du système, d'une part, et dans les performances des solutions calculées pour le concrétiser, d'autre part. De notre point de vue, rappelons que nous souhaitons un référentiel géodésique universel, de façon à permettre l'accès à celui-ci en tout point du globe, et aussi stable et exact que possible, pour permettre la détermination précise et sans ambiguïté de toute déformation réelle de l'écorce terrestre. En ce qui concerne l'accès au système, la configuration du réseau de points n'est peut-être pas encore optimale, néanmoins elle s'améliore clairement au cours du temps grâce en particulier aux nouvelles techniques radioélectriques portables et relativement bon marché. La couverture des sites de l'ITRF94 est indiquée dans la figure 73. Quant à la qualité du jeu de coordonnées combiné de l'ITRF, elle dépend notamment des données considérées et de la pondération choisie. Les indicateurs statistiques de qualité sont issus de la méthode des moindres carrés appliquée au modèle de combinaison choisi. En particulier, le facteur de variance unitaire nous renseigne utilement de l'adéquation entre les modèles fonctionnel et statistique adoptés et les données employées, et par suite du déroulement général du calcul. Les paramètres de transformation estimés donnent par ailleurs une idée du niveau de cohérence interne entre les solutions individuelles des centres d'analyse et la solution combinée ITRF. Il apparaît dans l'analyse de l'ITRF94 que les origines des différentes solutions présentent un accord de l'ordre de 1-2 cm dans la plupart des cas, et que les échelles sont cohérentes au niveau de 10-9, soit 6 mm à la surface de la Terre [Boucher et al, 1996].
L'exactitude du jeu de coordonnées combiné peut être évaluée à partir des résidus obtenus du calcul, autrement dit, à partir des différences entre coordonnées des solutions individuelles et coordonnées du jeu combiné après transformation à sept paramètres. Le terme d'exactitude n'est pas abusif dans la mesure où l'on considère des jeux de coordonnées provenant de techniques indépendantes de géodésie spatiale, en l'occurrence les plus précises du moment, et que leurs observations sont traitées par plusieurs centres d'analyse. L'intercomparaison des solutions individuelles de nature et d'origine variées est en effet le meilleur moyen de déceler l'existence d'erreurs systématiques au sein des techniques de mesure et des processus d'analyse des observations, et donc de stimuler les efforts de recherche pour les identifier et les modéliser.
Les rapports de l'analyse des solutions de l'ITRF présentent diverses synthèses de ces résidus, regroupés par sites géographiques ou par solutions individuelles, exprimés sans distinguer les composantes de l'espace ou en séparant les composantes horizontale et verticale, simples, normalisés, ou pondérés. Afin de donner des ordres de grandeur et une idée de l'évolution des performances des réalisations de l'ITRS, nous avons extrait des rapports techniques de l'IERS les résidus pondérés, sans distinction des composantes de l'espace, et regroupés par solutions individuelles. Ces résidus sont résumés dans le tableau de la figure 74 en donnant leur moyenne et les l'intervalles d'amplitude par technique et par repère. La dernière ligne du tableau permet d'apprécier la progression de la qualité des solutions de l'ITRF au cours du temps depuis la solution ITRF89. Nous ne devons pas cependant nous fourvoyer en identifiant ces chiffres à la valeur de l'exactitude du système de référence combiné pour au moins deux raisons. D'une part, les indicateurs construits à partir des résidus diffèrent de l'erreur moyenne quadratique, seul estimateur à prendre en compte en théorie les biais. L'erreur moyenne quadratique est d'ailleurs difficile à estimer de manière parfaite puisque les erreurs systématiques sont souvent inconnues. D'autre part, Sillard [1997-a] montre dans une étude récente la sensibilité des résultats de combinaison des jeux de coordonnées en fonction de pondérations empiriques jugées a priori satisfaisantes au regard des indicateurs classiques des moindres carrés. Il préconise à cet égard l'application d'une méthode rigoureuse d'estimation des matrices de covariance des jeux de coordonnées à partir de l'information a priori fournie par les centres d'analyse.
| Technique | ITRF89 | ITRF90 | ITRF91 | ITRF92 | ITRF93* | ITRF94* |
|---|---|---|---|---|---|---|
| VLBI | 2.5 [0.9 ; 6.1] | 0.9 [0.7 ; 1.5] | 0.9 [0.7 ; 1] | 0.8 [0.5 ; 1.5] | 0.6 [0.5 ; 0.6] | 0.9 [0.4 ; 1.9] |
| SLR | 5.2 [2.7 ; 10.8] | 3.0 [1.6 ; 5] | 3.2 [2.1 ; 4.4] | 2.7 [1.5 ; 5.8] | 2.0 | 1.1 |
| LLR | 6.0 [2.5 ; 14.4] | 3.1 [3 ; 3.2] | 4.3 [3.1 ; 6.6] | 3.5 [3.1 ; 3.9] | --- | --- |
| GPS | --- | --- | 1.4 | 1.4 [0.7 ; 3.4] | 1.0 [0.7 ; 1.3] | 1.1 [0.5 ; 2] |
| DORIS | --- | --- | --- | --- | --- | 2.2 [1.8 ; 2.8] |
| Moyenne | 4.5 cm | 2.3 cm | 2.5 cm | 2.1 cm | 1.2 cm | 1.3 cm |
Ainsi que le soulignent les auteurs des rapports de l'IERS concernés, les valeurs fournies ne cherchent pas à classer les techniques elles-mêmes, mais seulement les solutions incluses dans l'ajustement global de chaque ITRF. Le lecteur intéressé par ces résultats et leur obtention est invité à consulter ces rapports. Notons que les stations de l'ITRF94 sont classées en fonction de la confiance allouée à l'estimation de leurs coordonnées et vitesses. Quatre classes ont été définies:
