Nous avons appliqué la technique de régression linéaire aux séries temporelles des marégraphes qui présentent au moins dix années de données RLR. Les résultats sont exposés dans le listage de l'annexe B. Chaque ligne correspond à une série temporelle. Elle est repérée par un numéro séquentiel, de 1 à 714, suivi du nom de la station; de ses codes identifiants PSMSL et GLOSS; du nombre de moyennes annuelles RLR; de la période de temps associée, première et dernière moyenne annuelle; et des paramètres estimés qui nous intéressent: la tendance en mm/an; son écart-type en mm/an; la racine carrée du facteur de variance unitaire en mm; le coefficient de corrélation linéaire et le coefficient de variation, qui sont sans dimension.
L'histogramme de la figure 20 montre la distribution des tendances (vitesses) estimées. Le mode principal de variation linéaire du niveau moyen de la mer est une élévation d'environ 1-2 mm/an. Cependant, le nombre de valeurs positives et le nombre de valeurs négatives sont respectivement de 65% et de 45%. On constate que 64% des tendances se situent dans l'intervalle [-1,+4[ mm/an, et que 96% sont dans l'intervalle [-8,+11[ mm/an.
Figure 20 : Histogramme des vitesses estimées par calcul de régression linéaire appliqué à chacune des 714 séries temporelles du PSMSL de plus de dix données annuelles (146 séries sont GLOSS).
La carte de la figure 21 illustre la répartition géographique des 714 tendances du niveau de la mer que nous avons estimées. La longueur du symbole est proportionnelle à la valeur estimée, la couleur rouge indique une élévation du niveau moyen de la mer et la couleur bleu une baisse.
Figure 21 : Répartition géographique des tendances du niveau de la mer que nous avons estimées par régression linéaire sur les 714 séries temporelles marégraphiques de plus de dix données moyennes annuelles. La longueur du symbole est proportionnelle à la valeur estimée, la couleur rouge indique une élévation du niveau moyen de la mer et la couleur bleu une baisse.
Le nombre de stations dans l'hémisphère Nord (89%) est clairement supérieur à celui de l'hémisphère Sud (11%). Cette remarque reste valable pour le sous-ensemble GLOSS (cf. figure 22), seulement le quart des marégraphes GLOSS se trouvent dans l'hémisphère Sud.
Figure 22 : Idem que la figure 21, mais seules les données des marégraphes GLOSS sont représentées, soit 146 tendances du niveau de la mer.
Les tendances se répartissent sur une fourchette assez large de -29 mm/an à +39 mm/an. La distribution géographique des valeurs semble à première vue disparate, aussi bien à l'échelle mondiale que régionale, voire locale. La baisse et l'élévation du niveau de la mer se manifestent indifféremment dans les deux hémisphères. Les agrandissements des figures 21.a, 21.b et 21.c révèlent des tendances opposées en des sites pouvant se trouver relativement proches. C'est le cas des stations de KIDDERPORE (n[[ordmasculine]] 253) et de TRIBENI (n[[ordmasculine]] 254) dans le Golfe du Bengale, pour lesquelles nous obtenons respectivement - 6 mm/an et +39 mm/an, alors qu'elles ne sont séparées que d'une cinquantaine de kilomètres.
Figure 21.a : Aggrandissement de la figure 21 pour l'Amérique du Nord.
Figure 21.b : Aggrandissement de la figure 21 pour l'Europe.
Figure 21.c : Aggrandissement de la figure 21 pour l'Asie.
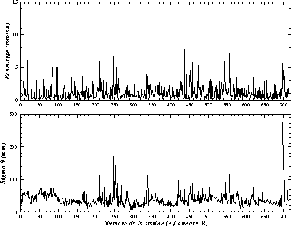
Le graphique de la figure 23 représente la valeur estimée de la tendance du niveau de la mer en fonction du numéro séquentiel de la station, tel qu'il est donné dans l'annexe B. Les valeurs numériques se répartissent effectivement autour d'une moyenne située entre 0 mm/an et 2 mm/an, avec une large dispersion. Toutefois, outre quelques estimations surprenantes, la plupart sont assez précises comme le témoigne l'histogramme de la figure 24. Ce dernier révèle que 62% des tendances sont déterminées avec un écart-type inférieur à 1 mm/an.
Figure 23 : Tendances du niveau de la mer et écart-types, estimés par ajustement linéaire appliqué aux 714 séries temporelles du PSMSL de plus de dix moyennes annuelles marégraphiques.
Figure 24 : Histogramme des écart-types des paramètres de tendance, estimés par régressions linéaires sur les 714 séries temporelles du PSMSL de plus de dix données annuelles marégraphiques (146 sont GLOSS).
En examinant attentivement l'allure de la figure 23, on remarque un signal qui ne correspond pas vraiment à un bruit blanc. Les points présentent parfois une certaine continuité, qui n'est pas liée au hasard car le PSMSL à ordonner son fichier de moyennes annuelles RLR par station le long d'une côte. La figure 25 découvre la localisation des stations numérotées de 41 à 90, qui, sur la figure 23, forment un pic singulier. Malgré une première impression, exacerbée par l'exemple de KIDDERPORE et de TRIBENI, une corrélation géographique semble exister parfois entre les résultats. Dès lors, les passages d'une côte à l'autre, ou vers les îles, peuvent expliquer certains écarts dans l'allure de la figure 23.
Figure 25 : Situation géographique des marégraphes numérotés de 41 à 90 dans l'annexe B.
Si l'on regarde l'écart-type du paramètre de tendance en fonction du numéro séquentiel de la station (cf. figure 26), aucun lien visible n'apparaît entre la précision de l'estimation indiquée par l'écart-type et la proximité géographique. En revanche, la racine carrée du facteur de variance unitaire, qui est un indicateur du niveau de bruit dans la série chronologique, semble attester des modulations régionales. Les erreurs instrumentales pouvant difficilement justifier ce comportement, l'explication se trouverait plutôt dans des phénomènes à caractère régional qui ne sont pas modélisés.
Figure 26 : Précision du paramètre de tendance et bruit dans l'enregistrement marégraphique, estimés respectivement par l'écart-type et par le facteur de variance que nous avons déterminés lors de la régression linéaire sur chacune des 714 séries temporelles ayant plus de dix moyennes annuelles.
La figure 27 permet d'étudier la relation entre la vitesse estimée et le nombre de moyennes annuelles présentes dans une série chronologique. Le graphique suscite au moins deux observations:
Toutefois, la première observation paraît contestée par un nuage de valeurs négatives qui ressort de la figure 27 au delà de 40 années. En remplaçant le symbole par le numéro du marégraphe auquel correspond la tendance, on s'aperçoit qu'il s'agit des stations de la figure 25, situées autour de la mer Baltique. Quant à la deuxième observation, la figure 28 montre en particulier que les séries chronologiques ayant plus de 30 moyennes annuelles ont un écart-type inférieur à 1 mm/an.
Figure 27 : Vitesses ou tendances du niveau de la mer, estimées par régression linéaire, en fonction du nombre de moyennes annuelles présentes dans les séries temporelles marégraphiques.
Figure 28 : Précision des paramètres de tendance du niveau de la mer en fonction de la longueur des séries temporelles marégraphiques associées. La précision est évaluée ici par l'écart-type du paramètre de tendance, issu de la régression linéaire.
Les observations ci-dessus confirment les conclusions de l'exercice de filtrage que nous avons réalisé dans la section précédente. Un nombre minimum de 30 années de données est nécessaire pour filtrer les variations interannuelles ou interdécennales, à caractère cyclique ou irrégulier, et estimer une tendance à long terme du niveau de la mer de manière précise. Les oscillations interdécennales de 20 années de durée ne sont pas rares, mais leur influence sur l'estimation des variations séculaires devient moins importante si l'on considère des séries temporelles longues. On s'affranchit alors de certaines erreurs d'interprétation.
Une partie de la corrélation géographique des résultats peut vraisemblablement être attribuée à ces oscillations interdécennales, provoquées par des phénomènes à caractère régional, comme par exemple celle que rapporte Barnett [1984] dans le sud-est asiatique. Mais la figure 29 révèle que, par ailleurs, il peut aussi exister une relation de dépendance géographique entre les vitesses déterminées avec précision à partir des séries de plus de 30 années de données.
Figure 29 : Tendances du niveau de la mer estimées par régression linéaire en fonction de la latitude géographique du marégraphe. La barre d'erreur représente la précision suvivant plus ou moins un écart-type du paramètre de tendance.
Les graphiques représentent les variations linéaires du niveau de la mer en fonction de la latitude des marégraphes. Leur allure témoigne de la présence d'un phénomène dont l'effet s'accentue à mesure que l'on progresse vers les latitudes élevées. Cet effet zonal devient clairement perceptible lorsque les séries temporelles couvrent plus de 30 années d'enregistrement, autrement il est noyé dans le bruit des résultats. Déjà repéré dans la figure 23, puis localisé dans la figure 25, il s'agit manifestement de l'effet du rebond postglaciaire dont nous parlerons plus amplement par la suite, notamment dans le chapitre III.
La dispersion des résultats de la figure 23 diminue nettement lorsque l'on élague les points des séries temporelles courtes (cf. figure 30). Aussi, les oscillations interdécennales contribuent pour une part non négligeable à la dispersion des tendances du niveau de la mer. L'allure du nouveau graphe ne révèle pas de nouvelles structures régionales hormis celle identifiée en mer Baltique. Tout au plus, on remarque une cohérence particulière des vitesses obtenues pour les marégraphes n° 622 à 688, qui échantillonnent la côte Est de l'Amérique du Nord, de la Floride à la Nouvelle Écosse.
Figure 30 : Tendances du niveau de la mer et écart-types, estimés par régression linéaire appliquée aux 292 séries temporelles marégraphiques du PSMSL de plus de trente données annuelles.
Mais le procédé d'élagage fondé sur des durées encore plus longues ne réduira pas davantage la dispersion des vitesses. Ceci est démontré sur le graphique en haut à droite de la figure 31, où sont représentés les résultats des calculs d'une tendance globale du niveau des mers à partir des tendances individuelles du niveau de la mer obtenues en chaque marégraphe par la régression linéaire. En ordonnées, nous avons donc la moyenne arithmétique simple d'un sous-ensemble de tendances individuelles, en abscisses la définition du sous-ensemble en question par le nombre minimum de moyennes annuelles que comportaient les séries temporelles. Les barres d'erreur indiquent la dispersion des tendances individuelles par rapport à la moyenne; elles correspondent à plus ou moins un écart-type.
Figure 31 : Estimations de la tendance du niveau des mers à partir de différents ensembles de données marégraphiques.
Les autres graphiques de la figure 31 sont construits suivant le même principe en considérant, soit le sous-ensemble plus restreint des vitesses fournies par les marégraphes GLOSS, soit un nouveau calcul de moyenne arithmétique où les vitesses sont pondérées par l'inverse de leur variance. L'examen de ces graphes soulève au moins deux observations:
Nous devons chercher l'explication de notre première remarque dans l'effet de la pondération qui consiste à accorder plus d'importance à certaines données. En l'occurrence, elle privilégie les vitesses estimées avec précision. Or, nous avons vu que celle-ci augmente avec la durée d'observation (cf. figure 28). Les valeurs des moyennes globales pondérées et leur barre d'erreur seraient déterminées essentiellement par les stations qui ont une longue série temporelle. Cette hypothèse semble confirmée lorsque l'on regarde le poids relatif des séries temporelles longues. Celui-ci est de 81% pour les 146 marégraphes de plus de 50 années de données, au lieu de 20% (146/714) dans le cas de la moyenne simple, et de 54% pour les 50 stations de plus de 80 ans au lieu de 7% (50/714). Ce poids relatif augmente au fur et à mesure que le sous-ensemble est restreint à des séries chronologiques plus longues. On comprend alors que les résultats des calculs pondérés varient si peu en fonction de la durée d'enregistrement minimale, bien que le nombre de marégraphes change considérablement.
En ce qui concerne la remarque sur les valeurs plus élevées obtenues pour les sous-ensembles GLOSS, elle s'expliquerait par le meilleur échantillonnage de la surface des océans. En effet, le jeu de stations GLOSS évite la surabondance des marégraphes dans une région donnée. Or, le nuage de points que nous avons identifié auparavant dans la figure 27 montre que les stations autour de la mer Baltique ont, d'une part, une couverture temporelle importante, et d'autre part, des vitesses estimées avec précision. En outre, elles représentent 23% de l'ensemble des stations ayant plus de 30 moyennes annuelles. Leur influence par leur nombre est aussi visible dans le graphique en haut à droite lorsqu'on n'utilise pas de pondération particulière. La moyenne globale diminue à partir du seuil de 30 moyennes annuelles. Par ailleurs, les marégraphes de la mer Baltique semblent responsables de la plus grande dispersion des tendances individuelles du niveau de la mer.
L'analyse préliminaire des variations linéaires indiquées par les marégraphes ne met pas clairement en évidence un signal eustatique, tel que celui que l'on attend d'un réchauffement climatique. La large dispersion des valeurs d'élévation ou de baisse du niveau de la mer ne peut vraiment être attribuée aux seuls changements de volume d'eau dans les océans. Les estimations des marégraphes varient parfois de manière continue d'un site à l'autre, suggérant une corrélation géographique, et parfois de manière abrupte entre deux observatoires proches. Outre les fluctuations interdécennales du niveau de mer, les mouvements de l'écorce terrestre sont en mesure d'apporter une explication réaliste dans les deux cas de figure. Les marégraphes fournissant des données relatives du niveau de la mer par rapport à une référence locale liée à la surface terrestre, ils enregistrent aussi les mouvements verticaux de celle-ci. L'origine de ces mouvements peut être très variée: isostasie, sédimentation, tectonique... de même que leur champ d'action. Nous verrons qu'ils présentent souvent un comportement linéaire sur les périodes de temps que nous considérons, et que leur amplitude est en général faible, mais, dans certains cas, suffisante pour masquer un signal eustatique.
